标题中提到的锁相环为三相锁相环,原理见此:三相锁相环(一)SRF-PLL算法参数设计、时域分析、频域分析与simulink仿真验证,本文不多赘述。
背景
现在很多锁相环很多是基于浮点数实现的,在一些高端的DSP上运算速度尚且可以,而我在项目中用的16位单片机(dsPIC33EP)性能太弱鸡,单次的浮点运算就需要3us左右,网侧电压频率又很高(400~800Hz),使用浮点数计算根本跟不上网侧电压变化速度,因此必须通过其他方法来加速运算。
芯片对于数学计算的支持
经过对编译器文件一通翻找,我发现厂家对芯片提供了定点数数学计算库(libQ),可以很方便地计算正弦、余弦、开方等计算,同时(DSP库)也提供了向量、矩阵运算和加速版PID控制器支持。其运算输入和输出都是以定点数表示,因此我转去看了看定点数,在MCU仿真中测试了一下运算速度,发现比浮点数快了30+倍。初略计算后发现使用定点数全部替换浮点数计算后基本可以满足要求。
顺带一提,这里提到的两个库的定点数本质是int16类型,不是*_Fract、_Accum*定点类型。定点类型我只听说过,但一直没有用过。
探寻器件对定点数类型的支持
一是库中并没有提供单独两个定点数的运算支持,只提供了向量之间的运算(虽然这也可以对两个定点数进行计算),二是此前在翻阅芯片配套编译器手册时,我记得芯片支持语言层的定点数类型运算(即*_Fract/_Accum*类型),我认为这种更加规范的类型编译后在器件上可能会对运算有一定优化,因此决定探索一下器件的定点数类型。
在XC16编译器的手册上,我找到了器件的定点格式以及C数据类型。但是文中只是简单解释了一下类型和对应的定点数据格式,甚至没有解释如何打开这个定点数数据类型的开关,只是在编译器手册中简单提到要打开一个compiler switch,后来我在MPLAB中鼓捣了好久才发现如何打开。
在开启定点数数据类型支持后,新的问题又来了:
- 我需要用到的其他库里面提供的数学计算支持,但是只能计算本质为int16类型的定点数,对于语言层面的定点数数据类型无法正常计算。
- 器件不支持定点类型与int16(表示的定点数)之间的计算,也就是定点类型只能与定点类型进行基本计算(我记得这个是规范中规定的)。
如果要强制将定点类型与int16之间进行计算,那么数据类型会被转换,也就是定点类型会被转化int16类型,其转换结果永远为-1/0/1,造成计算结果是错误的。这一开始令我非常困惑,但是后来想了想其实这与浮点数转换成整数的逻辑是一样的,这样的设计也算是比较科学规范的。
作为探索的补充,把定点类型和int16之间进行转换的思路如下:以定点转int16定点数为例,先把定点类型取地址并转化为void类型指针,再转化为int16指针,最后再取值,即:int b = *(int *) (void *) &a。
我无法接受转换过程带来的时间消耗,在权衡之下只得放弃器件的定点数数据类型,选择直接用普通的int16实现定点数的基本计算,然后将器件未提供的一些基本运算用C实现。
由于int16定点数相当于把普通的数字扩大了2^15倍(32768),所以将两个定点数相乘后再缩小2^15得到的就是以定点数表示的乘积结果,在C代码中只需要先把两个int16转换为int32,然后再进行基本运算,最后右移15位转换为int16即可。
锁相环实现
因为需要遵循器件库函数输入要求、ADC精度不高、纯int32计算太慢,我的定点数采用int16数据类型,遵循Q15格式,即1个最高位用来表示符号,后面15位用来表示大小,这种格式可以表示范围在-1到1-2^-15(约0.99997,下文中近似为1)。
由于Q15定点数的表示范围限制,需要对模型进行修改,逐步定点化。
- 在simulink仿真中搭建好模型之后,将网侧输入适当缩放并留足空间,使其输入值始终在-1~1中。
- 修改PI控制器的参数,也确保其值在-1
1中。注意,在下图中,我的PI控制器输出的值为1内,分别对应到-π~π。 - 将模型内部各个模块的数据格式逐步设置为
fixdt(1, 16, 15),在MATLAB Function 模块中使用fi(x, 1, 16, 15)将运算中的数据转化为定点数,确保计算过程用的是定点数,个别难处理的地方可以酌情考虑用double算完后再转化为定点数。 - 修改积分器,使得积分结果不会溢出。我使用的策略是直接积分,如果积分结果大于等于
fi(1, 1, 16, 15),则将积分结果替换为fi(-1, 1, 16, 15);如果积分结果小于等于fi(-1, 1, 16, 15),则替换为fi(1, 1, 16, 15)。注意:此处积分器使用的是饱和加法,当两个定点数的和会溢出时,必定会返回定点数所能表示的最大值或最小值。再次注意:当两个fixdt(1, 16, 15)定点数和溢出时,matlab返回的不是旧格式了,而是fixdt(1, 17, 15)!
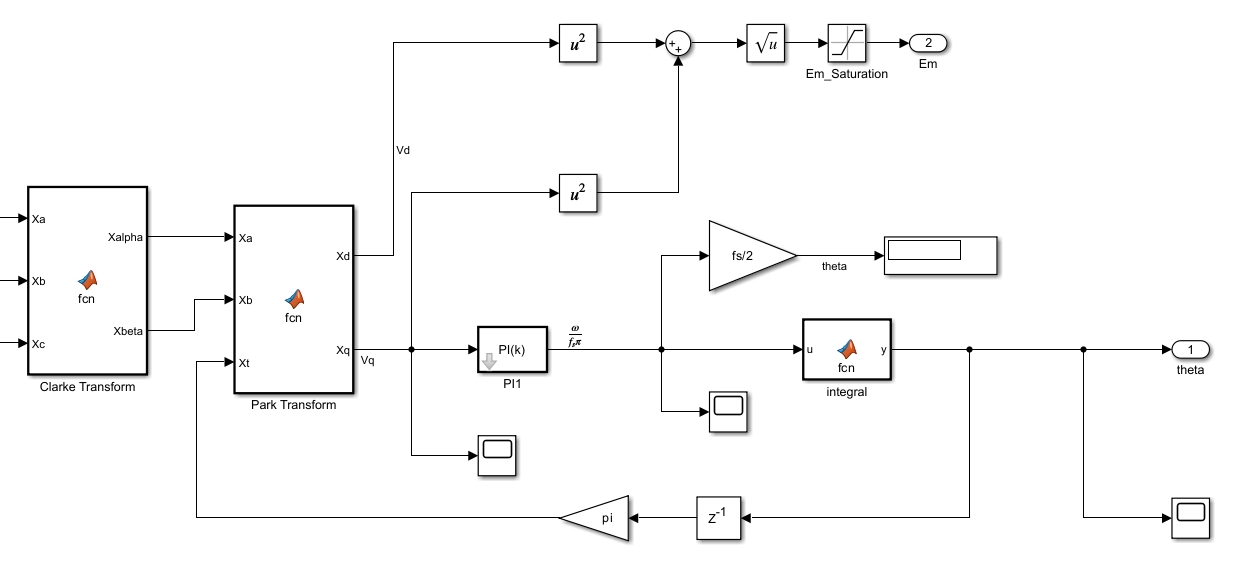
下图为PLL模型图,输入为网侧三相电压,输出theta为角度,此角度范围为[-1, 1],映射到[-π, π];输出Em为幅值。
下面是代码(非芯片上的代码,仅仅是在PC上仿真)。为了在PC上测试代码,我把芯片独有的一些库去掉(libQ和DSP库等用于辅助定点数计算的库),改用C模拟实现了,并写在头文件fit.h中,一并粘贴在文末。对于cos、sin、sqrt的计算我并未用查表法实现,而是偷偷用math库过度了,因此需要移植到其他单片机上时,还需要对代码进行修改。
1 |
|
fit.h
1 |
|
Preview: